Projects or Jump to Updates (click me)
Computer Science
-
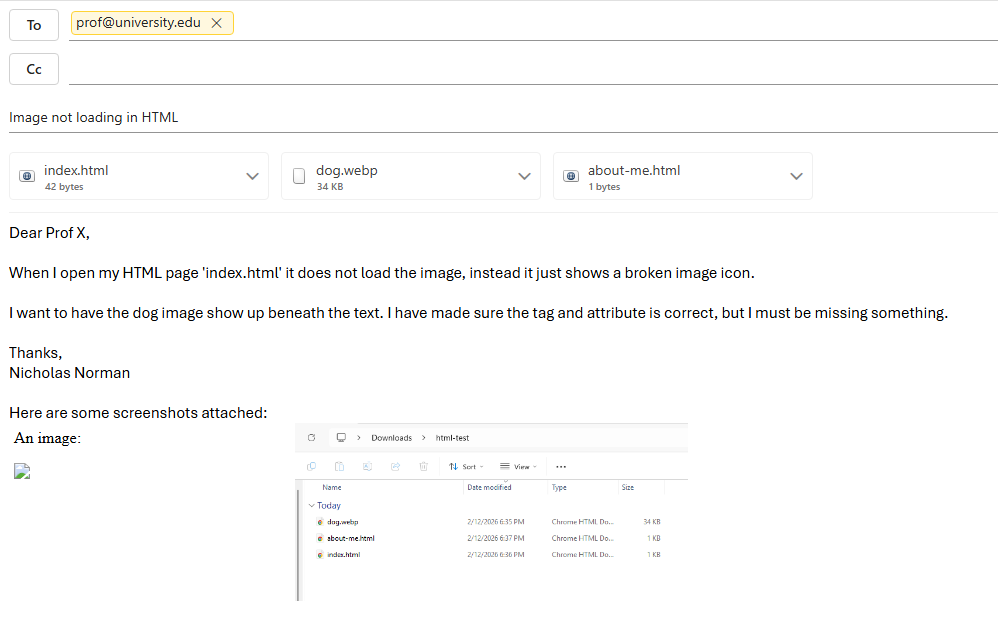
 Bottle Label Calculator Extension
Bottle Label Calculator ExtensionI made this to make my retail job easier. It counts the number of labels I need to print per case of bottle.
-
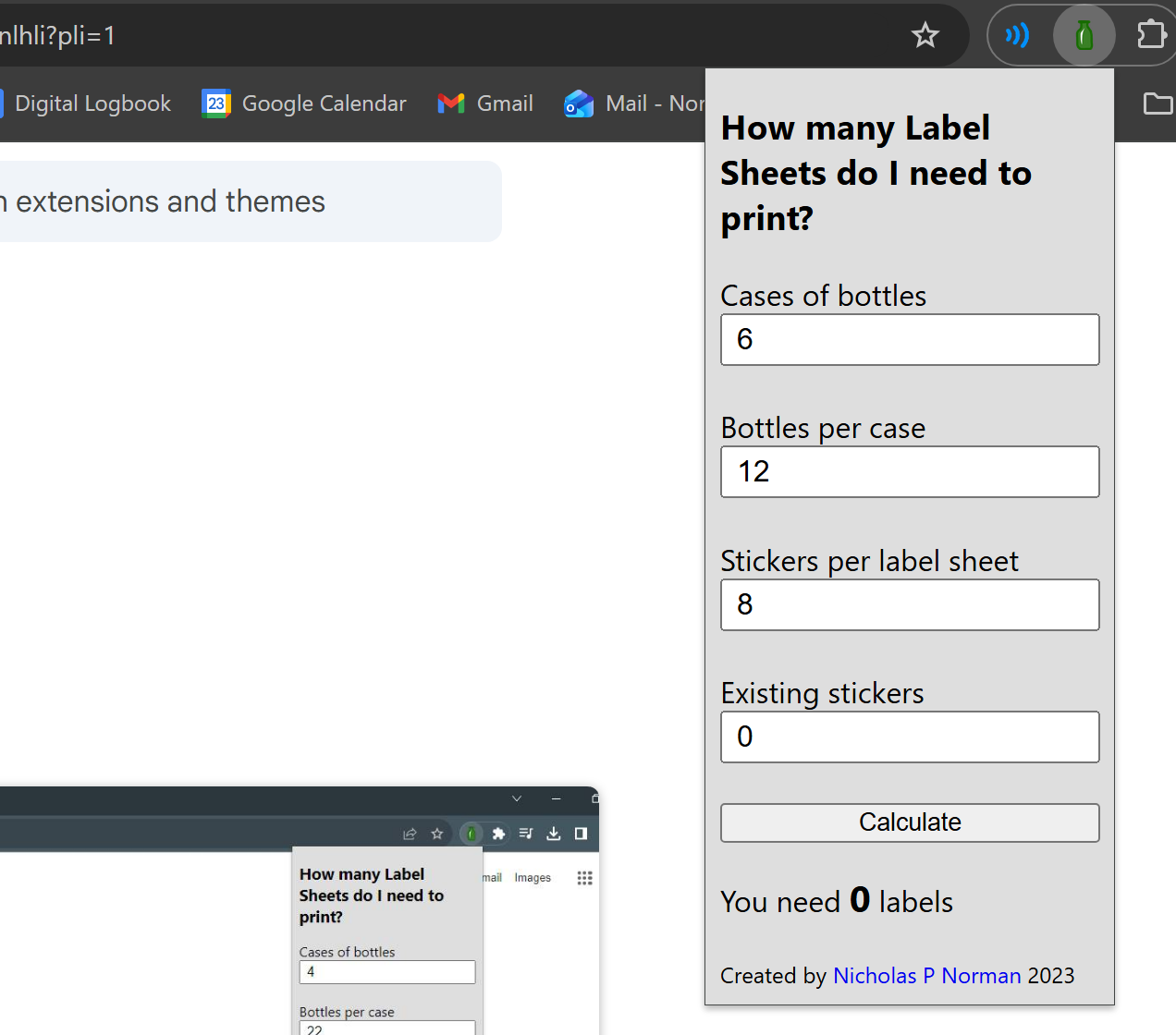
 Tic-Tac-Toe JS
Tic-Tac-Toe JSSimple, tic-tac-toe in JavaScript
-
 The PIN Game
The PIN GameA fun game where you try to guess all the codes.
-
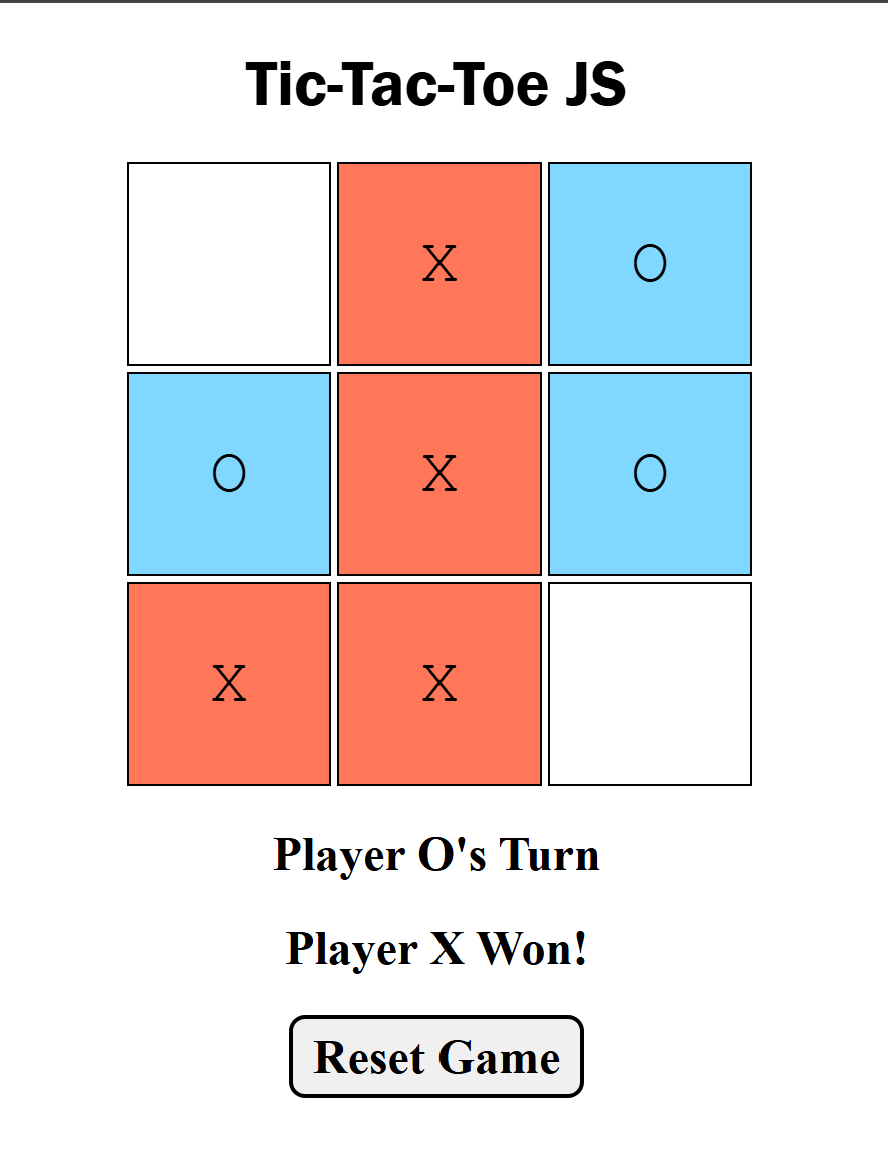
 Binary Calculator
Binary Calculator1 byte calculator for binary and two's compliment
-
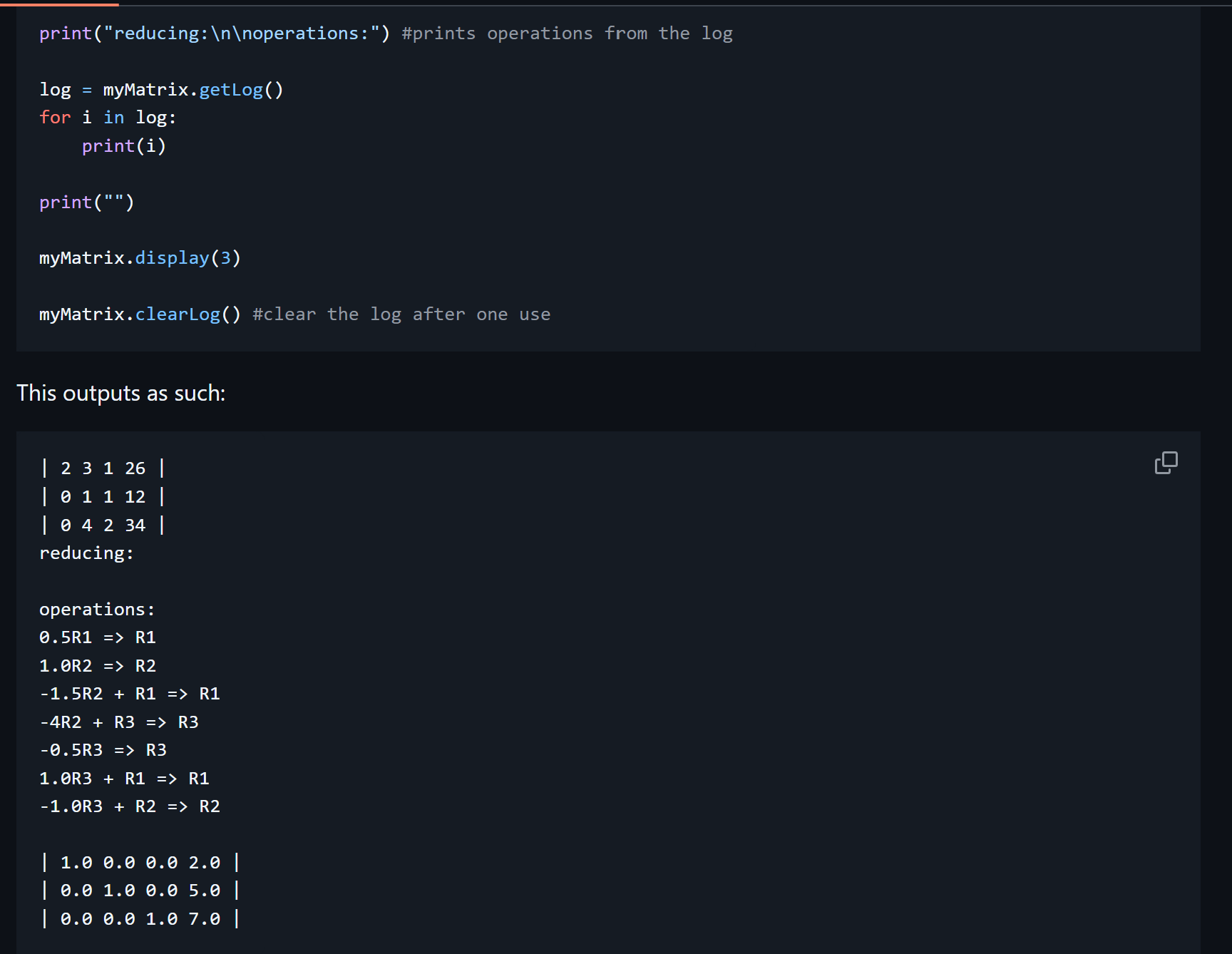 RREF Matrix Solver
RREF Matrix SolverA matrix object solved by (Row Reduced Echelon Form)
-
 Duodecimal Clock
Duodecimal ClockA base 12 clock! (24 hour and 12 hour at the same time!)
-
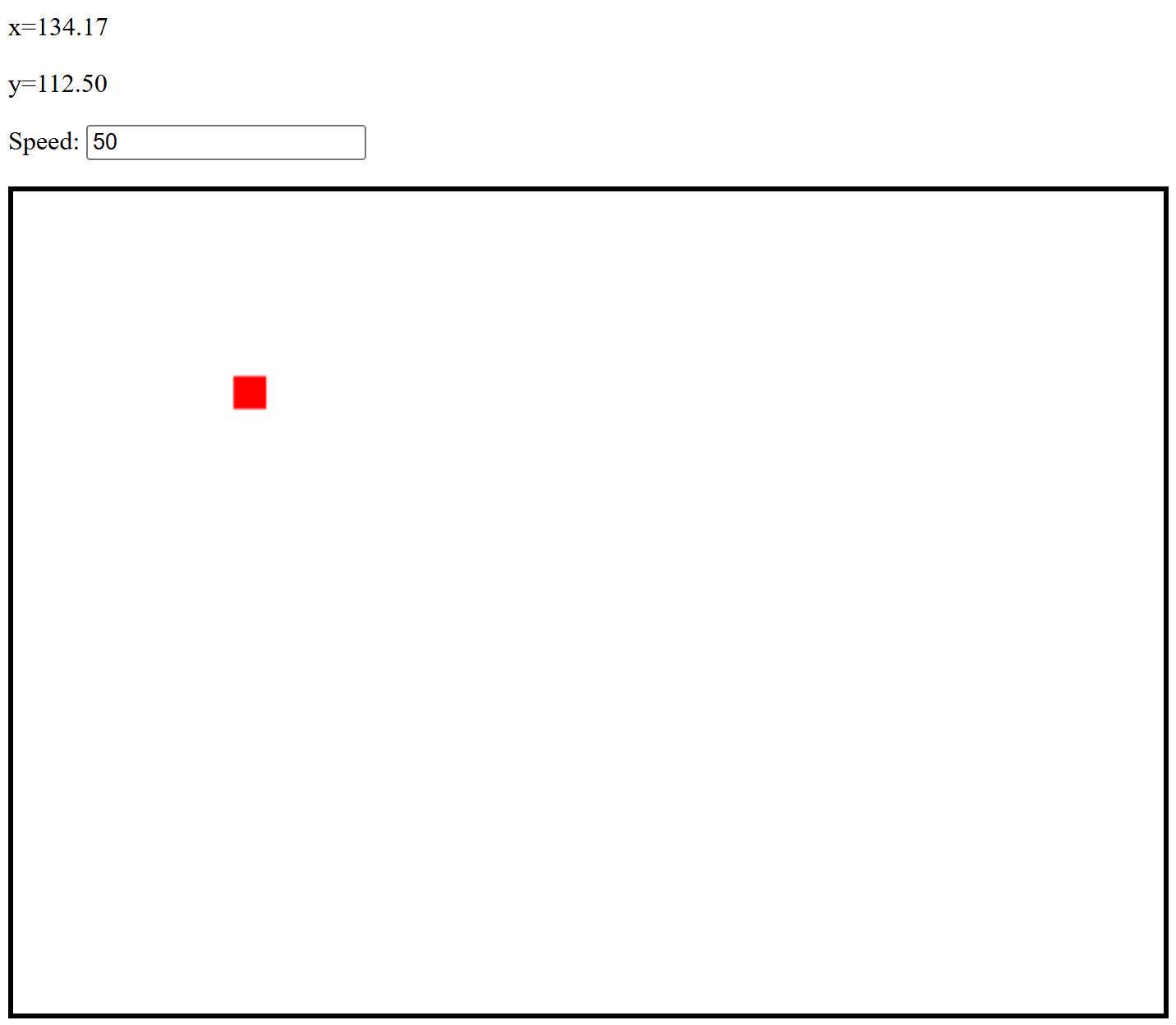 Game Movement Using JS Canvas
Game Movement Using JS CanvasRendering 2D game movment using JavaScripts builtin Canvas
-
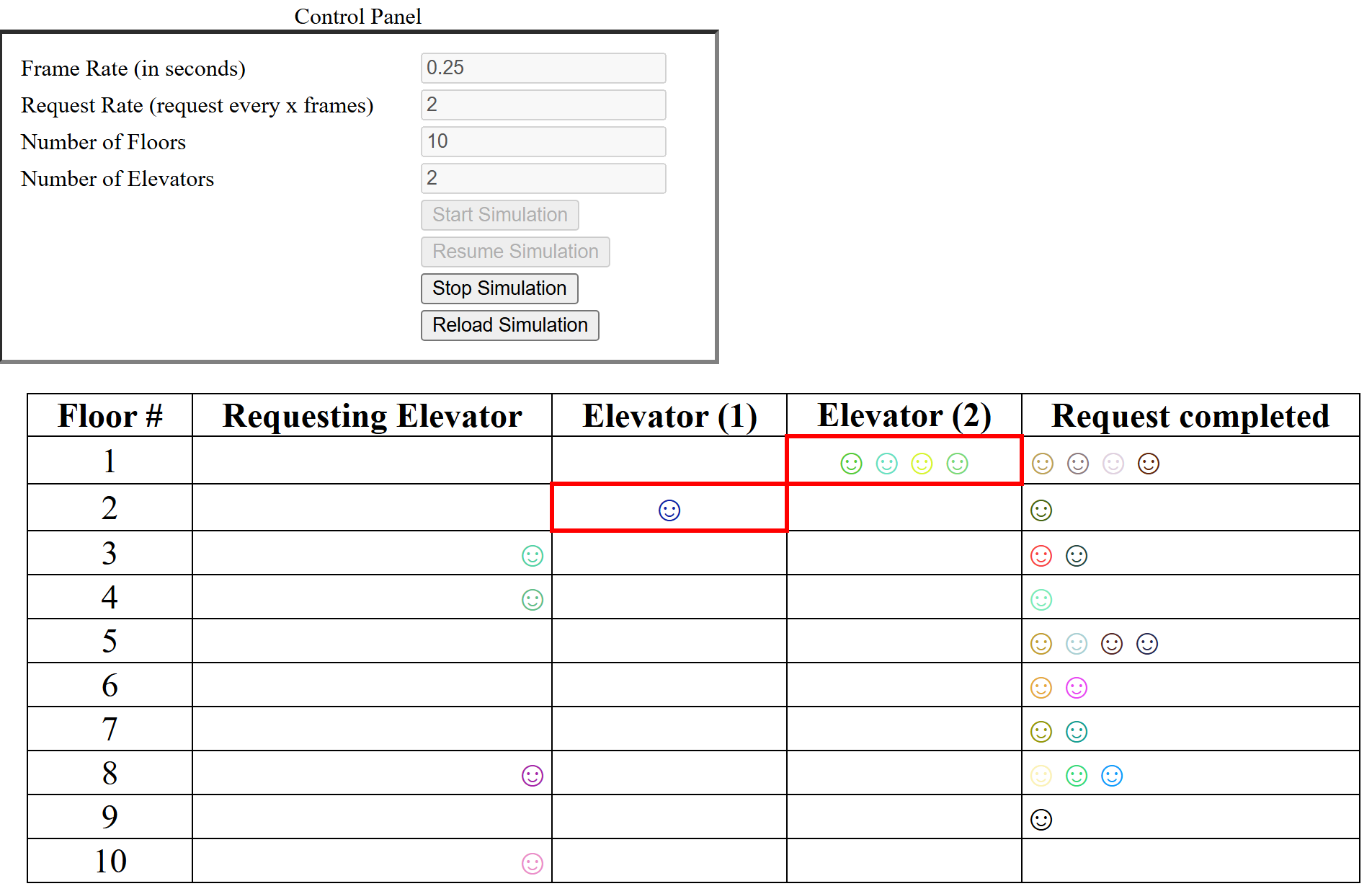 Elevator Simulator
Elevator SimulatorSimulate elevators
-
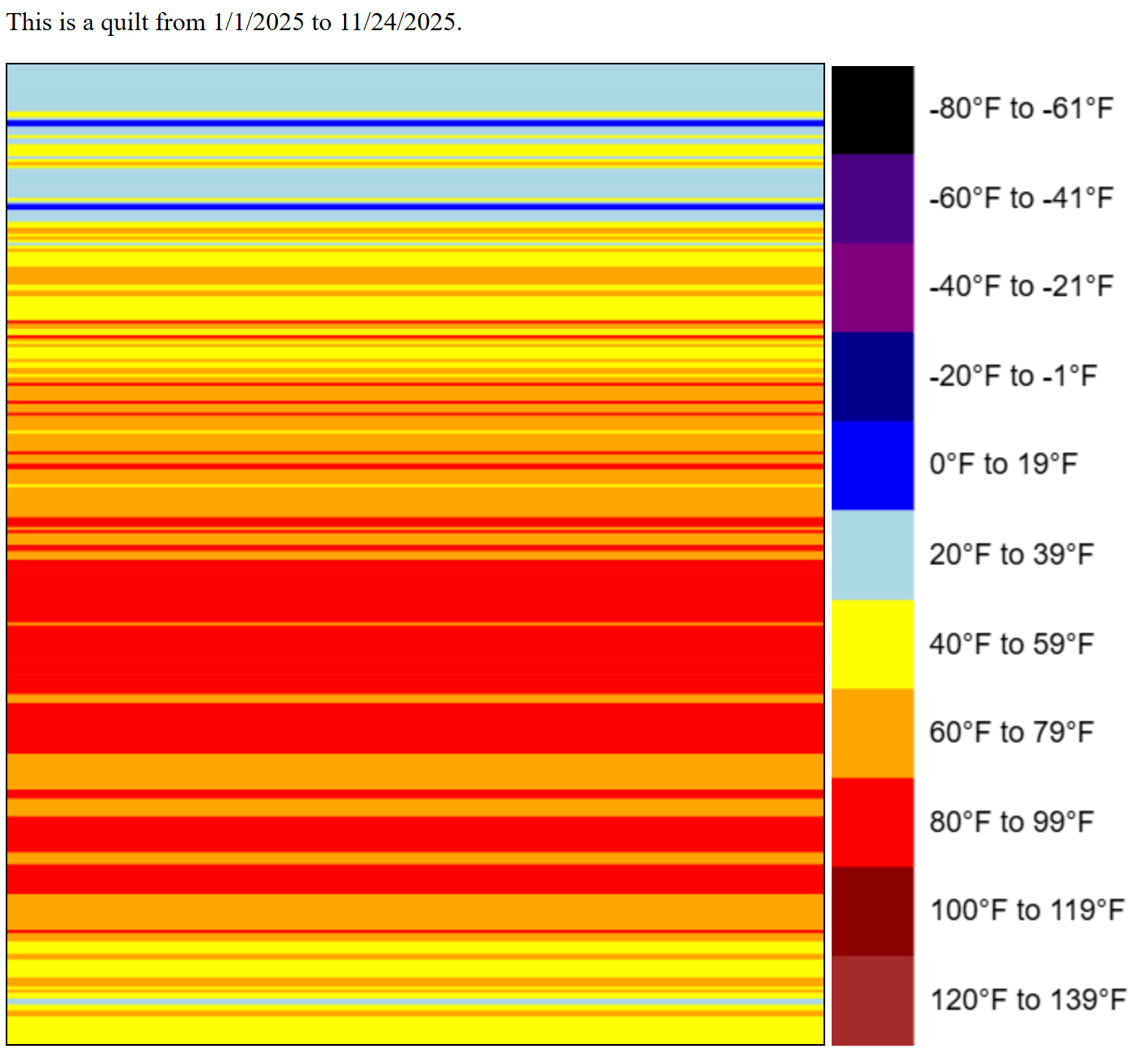 Temperature Quilt
Temperature QuiltBuild a blanket where each row represts that day's max temperature!
-
 Line of Time
Line of TimeA Chronology type game built for multiple people and to showcase any history! Use your own "cards" to teach and learn whatever history you want! Also use it for non-year values, such as area or volume.
-
 JS Renderer
JS RendererA 3D line renderer in JavaScript using weak perspective projection!
-
 Scratch-off
Scratch-offA mini-scratch-off game. Can you win?
-
 NAND2Tetris Assembler
NAND2Tetris AssemblerAn assembler for the HACK Computer built in the NAND2Tetris Course
-
 Bingo!
Bingo!A way to call bingo with only numbers
Research
-
 Paleoclimate Research Poster
Paleoclimate Research PosterI worked with the Multidisciplinary Undergraduate Research Institute.
Work In Progress
-
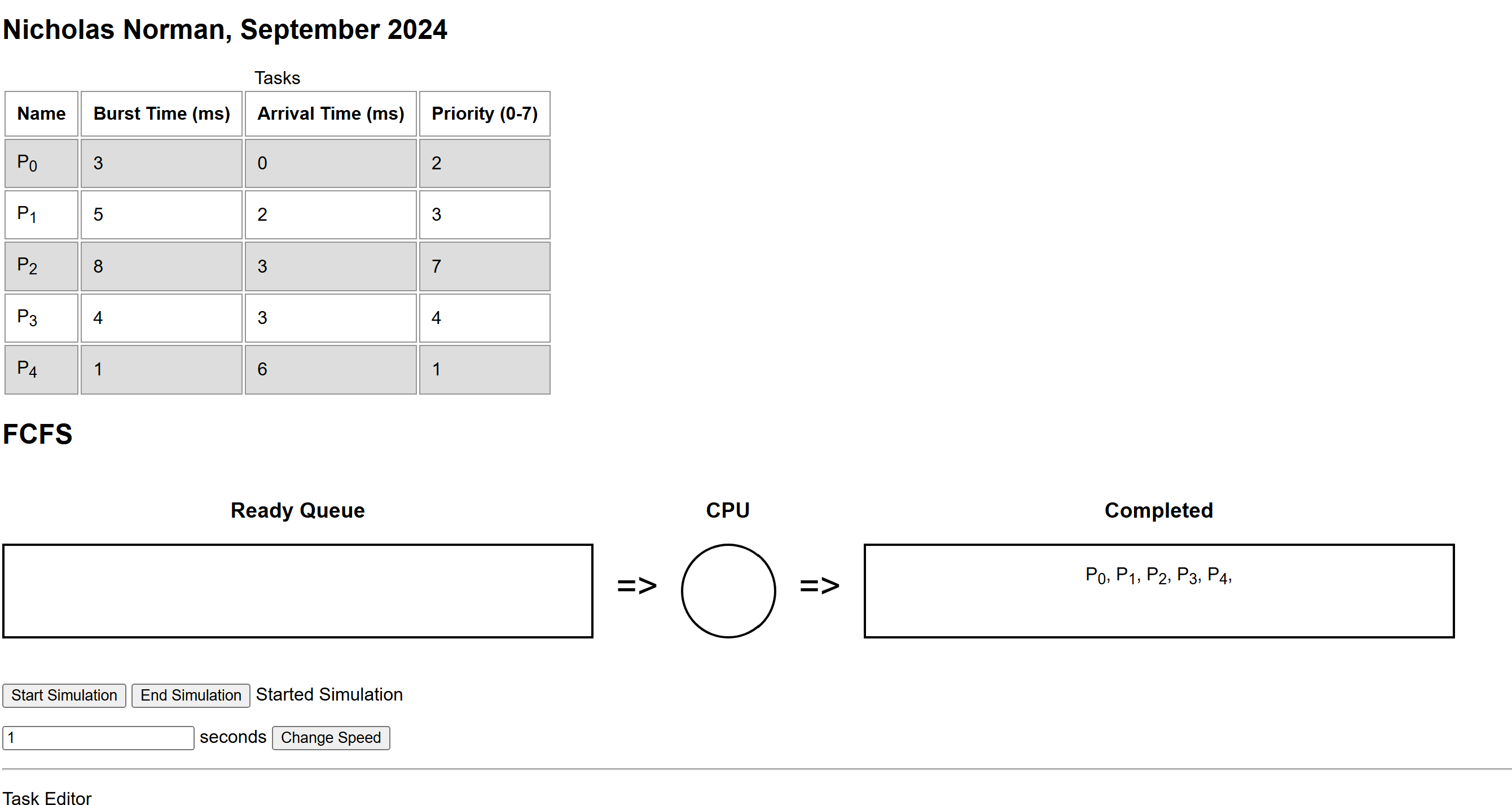 CPU Task Scheduling Simulator
CPU Task Scheduling SimulatorSimulate different task scheduling algorithms
-
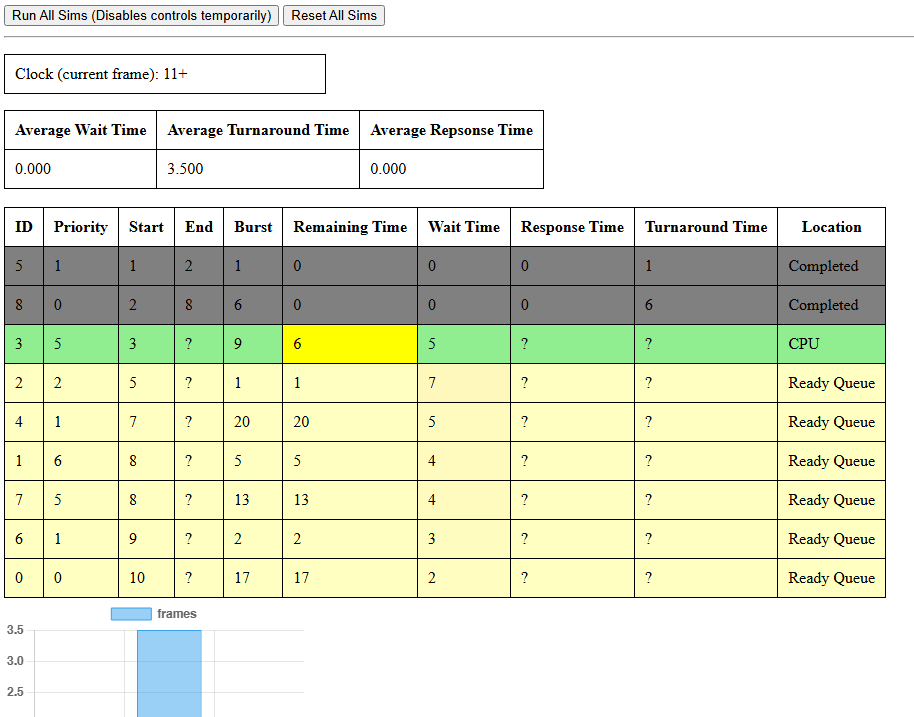 NEW CPU Task Scheduling Simulator
NEW CPU Task Scheduling SimulatorSimulate different task scheduling algorithms!
Games
-
 Bubble Wrap Pop
Bubble Wrap PopPlay in browser or download! Pop bubbles!
-
 American Santa
American SantaFight your way into the North Pole and stop Krampus... with your gun!
-
 Be the Pin! Bowling Simulator Remastered
Be the Pin! Bowling Simulator RemasteredBe the pin and avoid the bowling balls!
-
 Rabies Island
Rabies IslandRabies has broken out, can you save the mayor and escape safely?
-
 Ramen Noodle Nonsense
Ramen Noodle NonsenseMove the ramen bowl left and right around the screen to catch ramen ingredients and make the perfect soup!
-
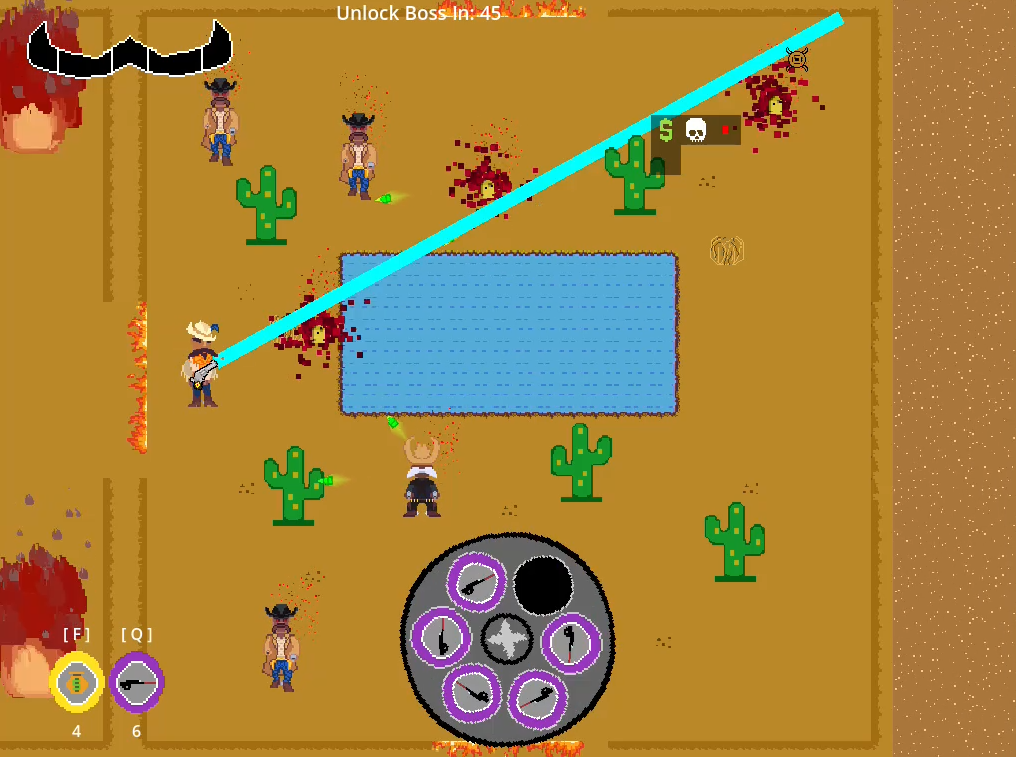 The Devil's Chamber
The Devil's ChamberUse your magical revolver along with special bullets while traversing the wild west to find and kill the Devil.
Thoughts, Updates, and Cool Stuff
Have thoughts on my thoughts? Email me at npn.not@gmail.com
2/10/2026 - IEEE Floating Point Standard
IEEE, or the Institute of Electrical and Electronics Engineers, is an American professional organization that comes up with standards used in many fields of electronics, including computers.
One such standard is the "IEEE Standard for Floating-Point Arithmetic." This document describes how floating point numbers, also know as floats, should be handled in binary. This document is quite verbose, coming in at 84 pages.
Here is a link to a PDF of IEEE Std 754-2019When I talk about this in class, I have a printed copy that I like to pull out. Even with two pages printed on each side, it still is quite a hunk of paper. This makes it seem like a pretty complicated topic. Why else would you need 84 pages?
Well it is actually easier to understand that you think. To just mess around with conversions, I found this handy converter that can show you what a decimal floating point number would look like in binary and the different parts.
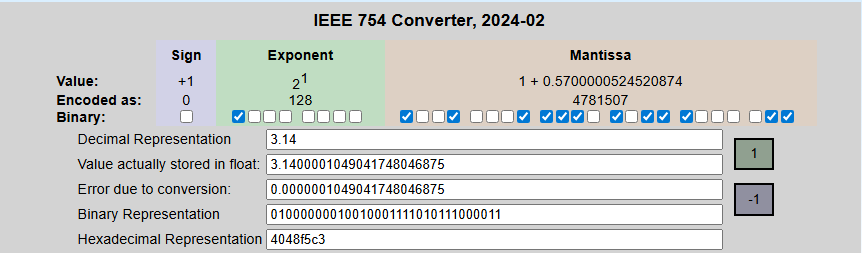
IEEE-754 Floating Point Converter
If this sparks your interest in learning about floating point numbers and you don't want to read the 84 page standard (why would you), then check out some videos online. Here's one from a creator that I quite like for these kinds of topics. See Spanning Tree's 'How Floating-Point Numbers Are Represented' as a good example.
1/15/2026 - Is Pseudocode Abstract or Concrete?
While reading Selected Papers on Computer Science by Don Knuth, I was struck with a realization. His explanation of an algorithm versus a program complements what should be taught in computer science classrooms. First, write the algorithm, then write the program. As he says, one algorithm may have many programs. To me that seems to make it harder to write the program first. You must not only come up with the algorithm, but the implementation (of many which are possible) as well.
"To me the word algorithm denotes an abstract method for computing some output from some input, while a program is an embodiment of a computational method in some language. I can write several different programs for the same algorithm [...]."
He continues on to say
"[...] I don't know any way to define any particular algorithm except in a programming language."

Source: amazon.com
This statement surprised me. Maybe it is because of the strict definition of "an abstract method for computing" that is holding this definition of an algorithm back from a more general algorithm. Even so, would simply writing down steps to an algorithm in English suffice? Where does pseudocode fit into all of this. Does it count because its like a programming language? Well it's also very much like English too! If we broaden computing to doing some operation, could a recipe for chocolate chip cookies be an algorithm?
I think it makes sense to think of an algorithm thorugh a narrow lens and to study and look at algorithms in a computer science or mathematics sense. Although, maybe the recipes and the English steps are how we can program our brain!
I think Knuth may argue that all of my examples are still embodiments of an algorithm, just more abstract or ambigious than a programming lanugage. How does that fit into the idea of writing the algorithm first, then programming it? Well, if the psuedocode I wrote is now considered a program, will I ever be able to represent the algorithm without some approximate representation? This is diving into a more philosophical problem of an abstract idea and its concrete representation (Philosophy Now, "Plato: A Theory of Forms").
The concept of 2 is represented by the number 2. It can also be represented by II or two (and many more). Even 10 in binary. It's hard to distinguish the concept from the representation. After further introspection, I may agree with Knuth on this point more than I had thought. So when we teach students to come up with an "algorithm" first, we may really mean to represent the algorithm in a higher-level sort of "program" (psuedocode), as to allow for ambiguity that will be removed when a more concrete "program" is written (C, C++, Python, Java). Even the set of steps we may call and algorithm, with some input and output, is really an abstract-like "program."
All this is to say, I was both surprised and intrigued by Knuth's definition. It took me from a concrete understanding to a not-so-concrete understanding, to Plato and forms, and back to a more practical way of thinking of "algorithms."
Selected Papers on Computer Science, "Algorithms, Programs, and Computer Science" Donald E. Knuth, 1996.
1/15/2026 - Conway's Surreal Number System
Recently, I watched a YouTube video about Surreal Numbers and the book written by Don Knuth (called Surreal Numbers), about a number system created by John Conway. After watching the video I was intrigued, so I went to the University Library and found a copy.
YouTube: Surreal Numbers (writing the first book) - NumberphileThe book can be hard to follow and I often times would need to write down examples to follow, but it was really fun going through it. It is written as a dialogue between Alice and Bill, two people who end up on an island and find a rock explaining an ancient number system. It explores their journey in uncovering this system similar to a mathematician discovering a new field of math, as Conway may have.
While I eventually bought my own copy, a copy can be found in a library or as a PDF online. Here is an excerpt about the rules of these surreal numbers, as found written on an ancient tablet. Note the humorous name change of John H. Conway as John H. W. H. Conway, in reference to the Hebrew name of god.
"In the beginning, everything was void, and J. H. W. H. Conway began to create numbers. Conway said, "Let there be two rules which bring forth all numbers large and small. This shall be the first rule: Every number corresponds to two sets of previously created numbers, such that no member of the left set is greater than or equal to any member of the right set. And the second rule shall be this: One number is less than or equal to another number if and only if no member of the first number's left set is greater than or equal to the second number, and no member of the second number's right set is less than or equal to the first number." And Conway examined these two rules he had made, and behold! They were very good. And the first number was created from the void left set and the void right set. Conway called this number "zero," and said that it shall be a sign to separate positive numbers from negative numbers. Conway proved that zero was less than or equal to zero, and he saw that it was good. And the evening and the morning were the day of zero. On the next day, two more numbers were created, one with zero as its left set and one with zero as its right set. And Conway called the former number "one," and the latter he called "minus one." And he proved that minus one is less than but not equal to zero and zero is less than but not equal to one. And the evening ..."

Source: amazon.com
1/14/2026 - A Computer "Bug"
A computer "bug," which is an actual moth, likely found by a member of Grace Hopper's team in the 1940's. As well the term referring to a bug as a mechanical defect was already in use, specifically by Thomas Edison.
 https://americanhistory.si.edu/collections/object/nmah_334663
https://americanhistory.si.edu/collections/object/nmah_334663
1/14/2026 - Grace Hopper's Compiler
Here is a good article I found while surfing the web titled "From Punch Cards to Python" which exlpores the history of Grace Hopper's A-0 compiler.
https://spectrum.ieee.org/from-punch-cards-to-python
1/14/2026 - GoTo Jail, Do Not Pass Go!
Ever wonder why GoTo went the way of the Dodo in high-level programming? Well, Edsger Dijkstra wrote a short paper in 1968 giving a great explanation of GoTo's faults using the concepts of mental load and textual and dynamic indices.
Go To Statement Considered Harmful, Communications of the ACM Volume 11, Issue 3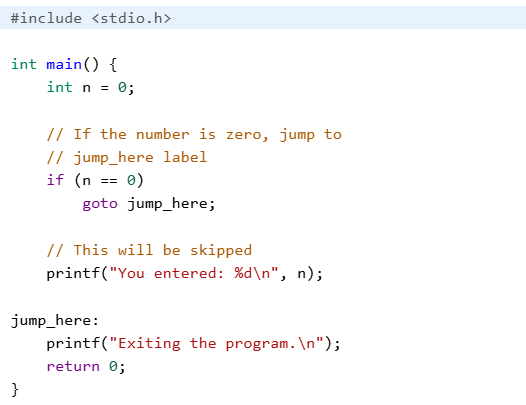
Source: geeksforgeeks